Table des matières
Cartographies du web
Utilisation de Gephi
Le logiciel Gephi est un logiciel gratuit de visualisation des données initialement développé par des étudiants de l’université de technologie de Compiègne (UTC) en 2008. C’est une application multi-plateforme disponible sous Windows, Mac OS X et Linux écrit en Java. L’utilisation de Gephi dans mon cas est très utile pour visualiser intuitivement les données récupérées aux étapes précédentes de l’étude, mais surtout pour isoler des singularités dans la structure de ces dernières.
En effet, Gephi possède plusieurs algorithmes de spatialisation afin de localiser les nœuds du graphe dans le plan, comme celui que nous utiliserons principalement pour la suite : ForceAtlas2. De plus, afin d’ajouter des dimensions visuelles à l’analyse des données, nous avons la possibilité d’utiliser des algorithmes de calculs statistiques issus de la théorie des graphes.
Spatialisation
Lors de mon étude, j’ai utilisé massivement l’algorithme ForceAltas2. Cet algorithme de spatialisation est basé sur un système physique où les nœuds s’expulsent les uns des autres (à la manière d’aimants) et les liens attirent les nœuds accrochés (à la manière de ressorts). Ces forces créent un mouvement qui converge à un état stationnaire final qui permet une interprétation visuelle des données. ForceAtlas2 possède la spécificité de placer les nœuds dans un plan 2D en fonction de la position des nœuds présent dans l’environnement, en se basant uniquement sur les connexions établies entre ces derniers (aucun autre attribut n’est pris en compte, si ce n’est la taille des nœuds et le poids des liens). Ainsi, les coordonnées d’un point ne représentent aucune variable spécifique à ce dernier, mais permet une visualisation graphique et intuitive de la structure du graphe difficilement interprétable initialement.
Cartographies
Pour réaliser les différentes cartographies suivantes, j’ai combiné l’algorithme de spatialisation précédent ForceAtlas2 avec différents algorithmes statistiques tels que HITS, ou PageRank. De plus, la couleur d’un nœud corresponds à la nationalité de ce dernier (qui est non capitalisée pour les sites upstreams ou downstreams : ils apparaissent en rose pâle pour être quasiment invisibles, mais apportent tout de même une influence lors de la spatialisation)
Nous pouvons noter que la densité du graphe est de 0,006 (tous nœuds compris), et de 0,032 (sans les nœuds upstreams et dowstreams). La densité représente le ratio de la quantité de connexions réelles du graphe (nombre de liens orientés) sur le nombre de potentielles connexions entre tous les nœuds du graphe. Plus cette valeur est faible et plus cela signifie que les nœuds sont relativement indépendants les uns des autres avec un graphe “éclaté”.
Etant donné que les nœuds upstreams et downstreams sont les extrémités du graphe, il est peut-être plus sage de ne pas les prendre en compte dans le calcul de la densité : en effet, il sont liés à d’autres sites, qui sont eux non présents car je n’ai pas capitalisé de données de upstream ou downstream de façon récursive pour ces derniers. On retiendra un calcul de densité de 0,032.
Utilisation de HITS
Hyperlink-Induced Topic Search (HITS) est un algorithme développé par Jon Kleinberg permettant le calcul de l’autorité d’une page web en fonction de son environnement. L’algorithme fourni pour chaque noeuds deux scores :
- Authority score : est d’autant plus élevé que le nombre de hubs différents qui référencent un nœud est grand. Ce score représente la valeur de l’importance d’un nœud au sein du graphe
- Hub score : est d’autant plus élevé qu’il pointe vers un grand nombre de nœuds avec une autorité importante. Ce score représente la valeur des liens présentés et leurs importance au sein du graphe
Dans le cas de nos données extraites du site Alexa.com, j’ai appliqué une taille des nœuds dépendante du score d’Authority ou Hub. Dans les deux cas, le graphe est très similaire est visible ci-dessous.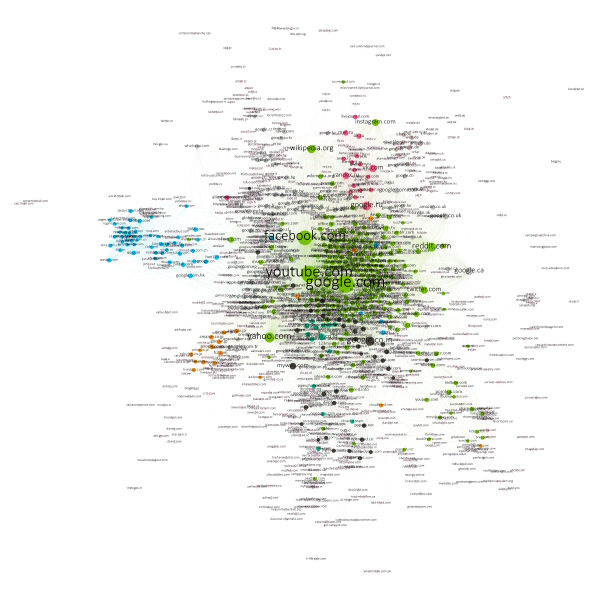
Utilisation de PageRank
L’algorithme PageRank permet à la base de mesurer quantitativement la popularité d’une page web. Il a été inventé par Larry Page et était initialement utilisé comme base de classement pour le moteur de recherche “Google”.
L’algorithme fonctionne en attribuant à chaque nœud un score proportionnel au nombre de fois que passe par cette page le programme, qui lui-même suis un chemin aléatoire, choisi, pour chaque nœud, suivant un des liens apparaissant sur celui-ci. Ainsi, un nœud possède un PageRank d’autant plus important qu’est grande la somme des PageRanks des nœuds qui pointent vers ce dernier. Ramené au web, Le PageRank est une mesure de centralité sur le réseau.
Dans le cas de nos données extraites du site Alexa.com, j’ai appliqué une taille des nœuds dépendante du PageRank. Deux cas sont déclinés :
- Avec les liens upstreams et downstreams
- En ne gardant que les sites du top 500

